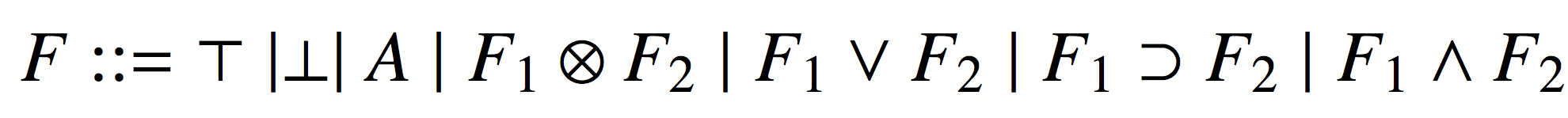
Prover for Full Lambek Calculus with Weakening and Bounded Contraction

The provers described in this page were implemented (and tested) in Maude 2.7. In a nutshell, an equational theory in Maude is used to specify the negative rules, which do not require backtracking. The positive rules are implemented as (conditional) rules in the module (a decision has to be taken to continue the proof).

The logic and the details of the proof system can be found at [CLOP16].

1. Full Lambek Calculus

We consider formulas build from the following syntax:
and proof rules:

2. Naive Prover

Download: FFLew2

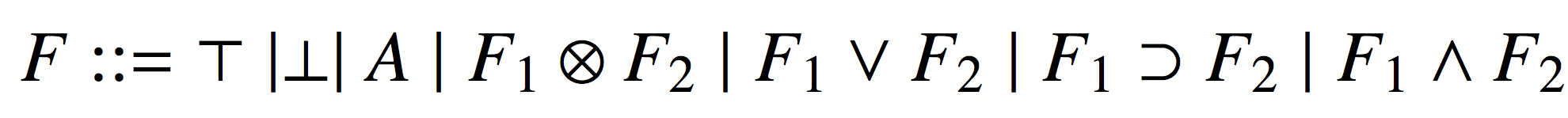
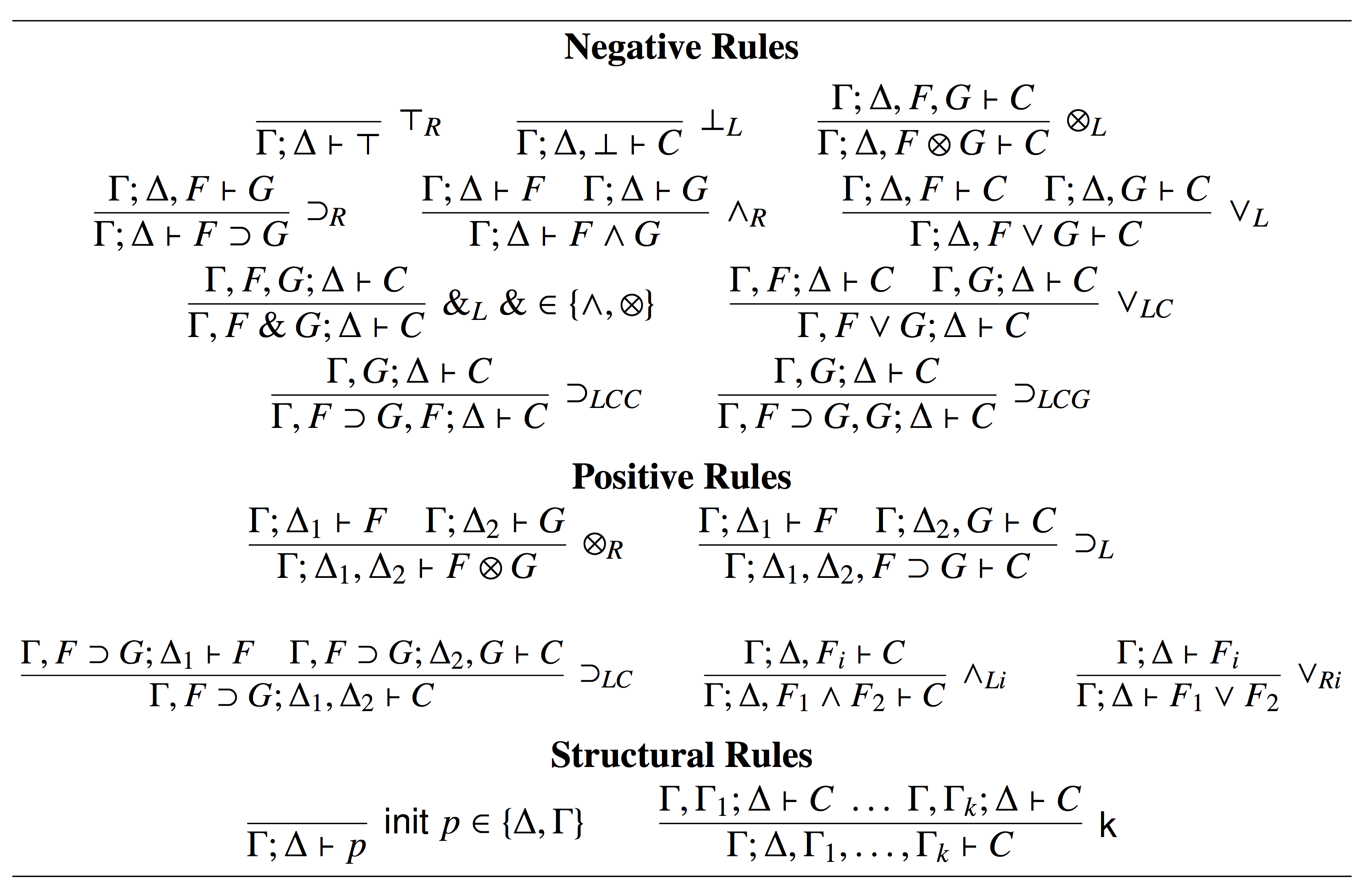
The first prover implements FLEW + 2-3 Rule and no lazy strategy is considered.

The prover can be invoked by:

maude flew_2.maude

Sequents has the shape [CC] LC ==> G where CC is the classical context, LC the linear context and G the goal.

Some examples:

search [1] [-] r, r -* p -* q, p -* q, (p -* q) -* (p -* q) -* (p -* q) -* s ==> s =>* proved .

search [1] [-] p -* bot, p -* q ==> (p -* q) * (p -* q) * (p -* q) =>* proved .

search [1] [-] r, p -* r -* q, p -* q ==> (p -* q) * (p -* q) * (p -* q) =>* proved .

search [1] [-] r, p -* r -* q, p -* q, (p -* q) * (p -* q) * (p -* q) -* s ==> s =>* proved .

search [1] [-] r, p -* r -* q, p -* q, (p -* q) -* ( (p -* q) -* ( (p -* q) -* s ) ) ==> s =>* proved .

search [1] [-] a, b, c, d ==> (a * c * c * a) + (b * d * d * b) =>* proved .

2. Lazy Splitting

Download: lazy-FLew2

Following the lazy system in [PP99] for linear logic [GIR87], the second prover implements a lazy strategy for the linear logic connectives. However, rule K is still non-deterministic. The prover can be used by typing:

maude lazy.maude

Some examples of use:

search [1] prove([-][r, (r -* p -* q), p -* q, ( (p -* q) -* (p -* q) -* (p -* q) -* s)] --> s) =>* PROVED .

search [1] prove([-][r, (p -* r -* q), p -* q] --> (p -* q) * (p -* q) * (p -* q)) =>* PROVED .

search [1] prove([-][r, (p -* r -* q), p -* q ,(p -* q) * (p -* q) * (p -* q) -* s] --> s) =>* PROVED .

search [1] prove([-][r, (p -* r -* q), p -* q, (p -* q) -* ( (p -* q) -* ( (p -* q) -* s ) )] --> s) =>* PROVED .

search [1] prove([-] [a, b, c, d] --> (a * a * c * c) + (b * d * b * d)) =>* PROVED .

search [1] prove([-][a, r, (p -* r -* q), p -* q, (p -* q) -* ( (p -* q) -* ( (p -* q) -* s ) )] --> s) =>* PROVED .

3. Lazy Splitting for Bounded Contraction

Download: LFLew2

By extending the idea of lazy splitting in linear logic (see, e.g., [PP99]), we developed a system that implements also lazy splitting for Bounded Contraction. The implementation is not longer "simple" and rules have to deal with complex input/output contexts:

The prover can be invoked by:

maude all_lazy.maude

Some examples:

search [1] prove(r, r -* p -* q, p -* q, ( (p -* q) -* (p -* q) -* (p -* q) -* s) --> s) =>* PROVED

search [1] prove(p -* bot, p -* q --> (p -* q) * (p -* q) * (p -* q)) =>* PROVED .

search [1] prove(a,b,c,d --> (a * c * a * c) + (b * d * b * d )) =>* PROVED .

search [1] prove(r, p -* r -* q, p -* q --> (p -* q) * (p -* q) * (p -* q)) =>* PROVED .

search [1] prove( r, p -* r -* q, p -* q, (p -* q) * (p -* q) * (p -* q) -* s --> s) =>* PROVED .

search [1] prove(r, p -* r -* q, p -* q, (p -* q) -* ( (p -* q) -* ( (p -* q) -* s ) ) --> s ) =>* PROVED .

Lazy application of K rule

There is also a prototypical implementation of the system implementing KLFL where K is eagerly applied (before the positive connectives). The code is here but is not stable for the moment.

4. References

[CLOP16] Agata Ciabattoni, Björn Lellmann, Carlos Olarte and Elaine Pimentel: From cut-free calculi to automated deduction: the case of bounded contraction. Submitted to LSFA'16 (2016). PDF
[GIR87] Jean-Yves Girard: Linear Logic. Theor. Comput. Sci. 50: 1-102 (1987)
[PP99] Pablo López and Ernesto Pimentel:Resource management in linear logic search revisited. In LPAR'99 (1999).